はじめに

点群からOriented Bounding Boxes (OBB)を推定します. PCAによる推定が高速で簡単に実装できますが, その性質上点群の分布に強く影響を受けるため品質は良くありません.

“Game Engine Gems 2"のFast Computation of Tight-Fitting Oriented Bounding Boxesを試してみようと思います. ヒューリスティックな方法で, 最適にはなりません.

アルゴリズム

1. 予め決めた方向に沿って最大最小距離の点を探し, できるだけ最大サイズの三角形を探索
2. 三角形の表と裏の方向に最大距離の点を探し, ２つの三角錐を探索
   • 探索した５点は凸包の点であるはずで, OBB上の点であるはずです
3. ６個の三角形の９辺について, 最も表面積が小さくなる直行座標を探索
   • 探索は全点群ではなく, 1.で探索した点だけが対象です
4. 3.で見つかった直行座標でOBBを推定

最大三角形の探索

決めた方向で探索します. 論文では6から13方向が示されていますが, 経験則の方法ですので正しい方向はないです. アルゴリズムは単純です.

1. 方向に沿って最も離れた２点を探索
2. ２点を通る直線から最も垂直距離が離れた点を探索

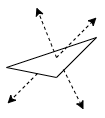
２つの三角錐

三角形の表裏に対して, 法線方向に最も離れた点を探索します.

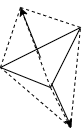
直行座標の推定

三角錐２つについて, 直行座標を計算し表面積を求めます. 最も小さな表面積の直行座標がOBBの軸の候補になります.

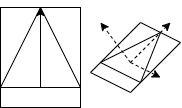
三角錐の各辺について, 直行する方向と三角形の法線で直行座標系を作ることができます. この座標で点群を包むAABを作り表面積を計算します.

OBB推定

推定したOBBの軸について, 最大最小の点を計算しOBBを推定します.

結果

疑似乱数で60001点を生成し, ２つのグループに分けて乱数で回転してみました. これでもPCAに有利なデータだと思います. このような見た目になります.

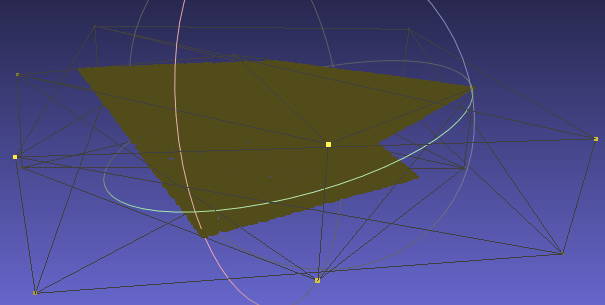
1000回繰り返して計測してみます.

方法	時間平均 (microseconds)	時間最大 (microseconds)	表面積平均	表面積最小	表面積最大
PCA	807	2420	890473.380063	308263.093750	1600693.750000
DiTo	1382	3729	633498.003234	253161.078125	1119446.250000
DiToSimd	960	3556	633498.003781	253161.093750	1119446.250000

まとめ

データ的にもPCAが有利で, イレギュラーなケースについてPCAは何もしていないです. それでも, よりタイトな結果を計算できるのは有用ではないでしょうか.